Cross-Correlation

Apply SciPy's correlate() to the waveforms of antenna pairs to determine incoming signal directions. More...

Functions
pl.DataFrame	supply_azimuthal_angle_masks (pl.DataFrame skymaps)
	Supplies azimuth masks to any sky map (eg time delay maps or correlation maps)
pl.DataFrame	combine_time_delay_maps_and_waveforms (pl.DataFrame masks_and_skymaps, pl.DataFrame waveforms)
	Prepares a big table that has all the column needed by cross_correlate.
pl.DataFrame	cross_correlate (pl.DataFrame big_frame)
	Compute the zero-centered normalized cross correlation (ZNCC) and makes correlation skymaps.
[float, float]	_get_true_direction (ROOT.pueo.Dataset dataset)
	Returns the true signal direction.
None	plot_correlation_map (pl.DataFrame correlation_frame, str plot_name, true_phi=None, true_theta=None)
	Plots the reult of cross_correlate.

Detailed Description

Apply SciPy's correlate() to the waveforms of antenna pairs to determine incoming signal directions.

Function Documentation

supply_azimuthal_angle_masks()

pl.DataFrame supply_azimuthal_angle_masks

(

pl.DataFrame

skymaps

)

Supplies azimuth masks to any sky map (eg time delay maps or correlation maps)

Parameters

[in]

skymaps

columns A1_PhiSector and A2_PhiSector are required

Return values

phi_masks

see the schema of the example output below

• Parameters:
  • Input: required columns are the \(\phi\)-sectors of the antenna pairs, A1_PhiSector and A2_PhiSector.
  • Output schema: one column (masks) will be attached to the input dataframe,

    $ A1_PhiSector                    <u8>
    $ A2_PhiSector                    <u8>
    $ masks        <array[bool, (1, 360)]>

• Explanation:
  • \(\phi\)-sector 1 is centered around 0 degrees azimuth, \(\phi\)-sector 2 around 15 degrees, and so on and so forth; the last \(\phi\) sector (24) is centered around 345 degrees.
  • Based on the antenna's field of view, the values outside a certain range are dropped.
  • In the figure below, we show what this would look like for antennas from the first three and the last \(\phi\)-sectors (white means masked).

Example masks of a few phi-sectors

• The chosen masking behavior for now is that only the data within the overlapping unmasked range would be kept.
• For instance, suppose an antenna from \(\phi\)-sector 1 is paired with an antenna from \(\phi\)-sector 2, then:

Example superimposed masks

Warning

• Thus, if the antenna pair's fields of view do not overlap, then everything will be masked.

Definition at line 34 of file locate_signal.py.

combine_time_delay_maps_and_waveforms()

pl.DataFrame combine_time_delay_maps_and_waveforms	(	pl.DataFrame	masks_and_skymaps,
		pl.DataFrame	waveforms )

Prepares a big table that has all the column needed by cross_correlate.

Parameters

[in]	masks_and_skymaps	The output of supply_azimuthal_angle_masks
[in]	waveforms	The output of waveform_plots.load_waveforms

Return values

big_frame

See sample output schema below.

• Parameters:
  • The following columns are required in waveforms:
    1. AntNum
    2. waveforms (volts)
    3. step size (nanoseconds)
    4. Pol
  • The following columns are required in masks_and_skymaps:
    1. A1_AntNum
    2. A2_AntNum
    3. time delays [sec]
    4. masks
  • The output schema:

    $ A1_AntNum                               <enum>
    $ A2_AntNum                               <enum>
    $ Pol                                     <enum>
    $ A1_waveforms (volts)        <array[f64, 3072]>
    $ A2_waveforms (volts)        <array[f64, 3072]>
    $ time delays [samples] <array[i64, (180, 360)]>
    $ masks                  <array[bool, (1, 360)]>

• Explanation:
  • time delays [samples] refers to the time delay skymaps, with the units converted from seconds to "samples"
  • That is, the units are in "steps" (step size (nanoseconds))
  • The values in these time delay skymaps are therefore integers, serving as indices.
  • These indices are then used later in cross_correlate when creating the correlation skymaps based on the time delay maps (via "fancy-indexing").
  • Qualitatively, the time delay maps have not changed. For example:
    Time Delay Map in Seconds
    Time Delay Map in Samples

Definition at line 149 of file locate_signal.py.

cross_correlate()

pl.DataFrame cross_correlate

(

pl.DataFrame

big_frame

)

Compute the zero-centered normalized cross correlation (ZNCC) and makes correlation skymaps.

Parameters

[in]

big_frame

The output of combine_time_delay_maps_and_waveforms()

Return values

correlation_maps

See the schema of the example output below

• Parameters: columns correlation and correlation maps will be added to the input, so the output schema looks like

  $ A1_AntNum                               <enum>
  $ A2_AntNum                               <enum>
  $ Pol                                     <enum>
  $ A1_waveforms (volts)        <array[f64, 3072]>
  $ A2_waveforms (volts)        <array[f64, 3072]>
  $ time delays [samples] <array[i64, (180, 360)]>
  $ masks                  <array[bool, (1, 360)]>
  $ correlation                 <array[f64, 6143]>
  $ correlation maps      <array[f64, (180, 360)]>

  • correlation maps contain correlation skymaps. These are matrices with the same dimensions as the time delay maps of time delays [samples], as the former are made based on the latter via "fancy-indexing"
  • Each matrix element of a correlation skymap is the correlation score between two waveforms, given some particular time delay, ie. phase shift.
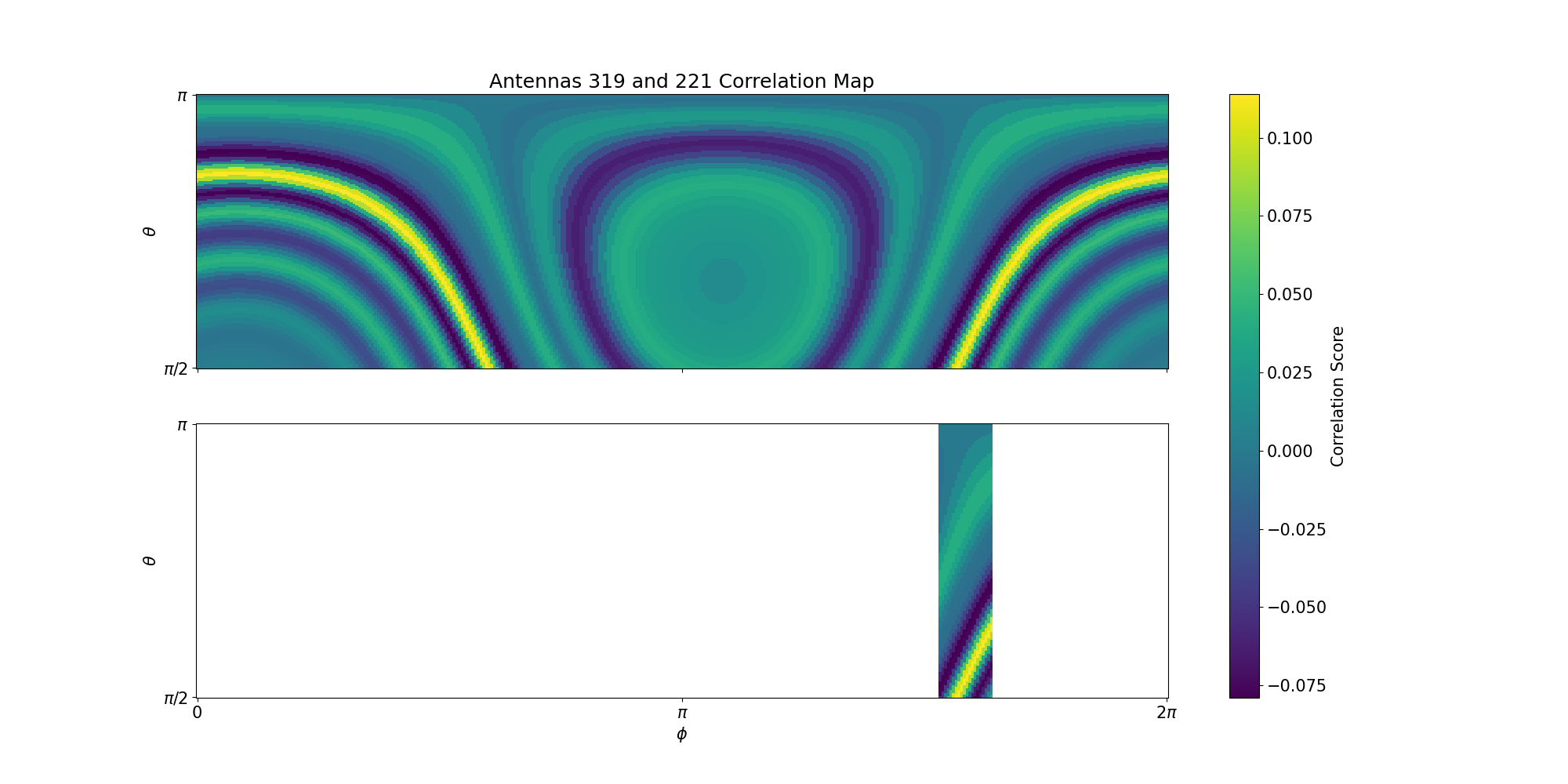
  • masks can be used to mask the correlation maps, as shown in the bottom subplot in the Figure above. The masks are defined by supply_azimuthal_angle_masks.

• Explanation:
  • Consider two waveforms,
    
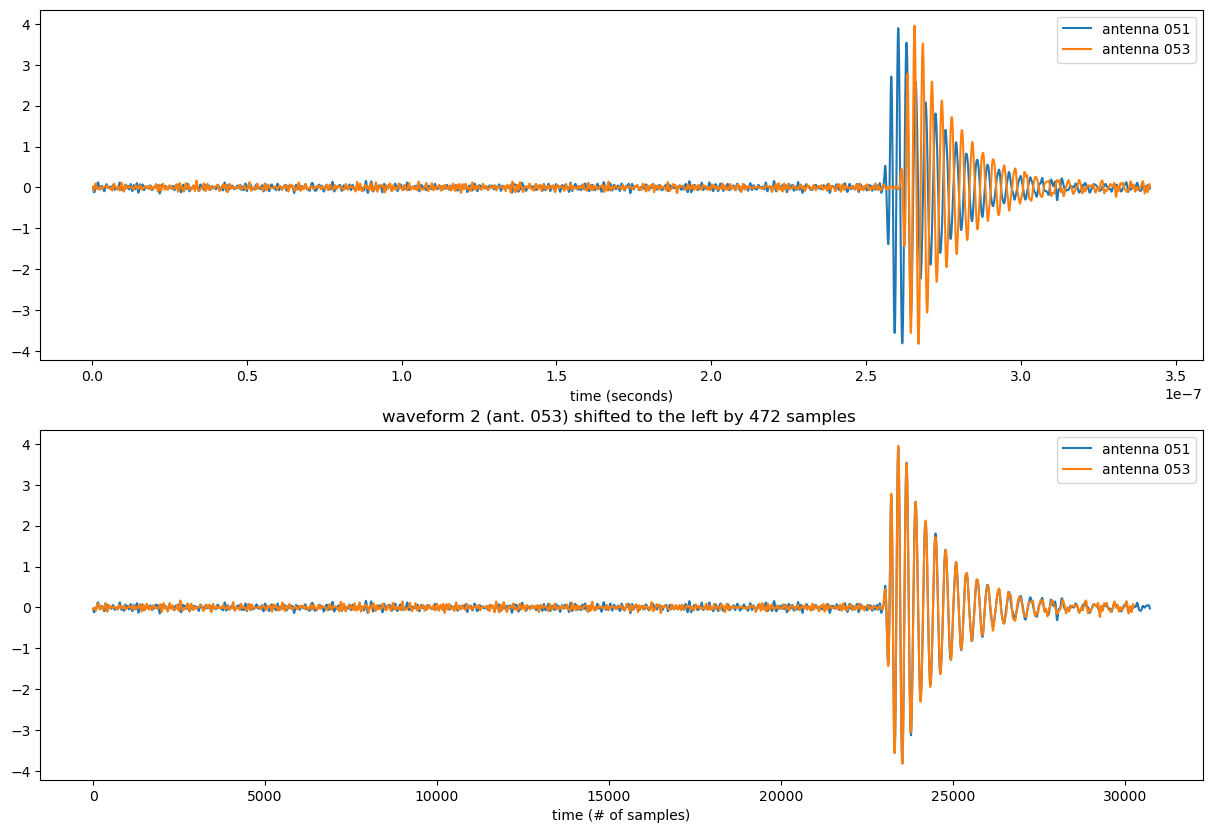
  • Each row in the correlation column is an array of correlation scores.
  • By shifting the waveforms we may be able to get them to align perfectly, at which point maximum correlation is achieved.
  • The correlation score tells us how "aligned" the two waveforms are after we phase shift A1_waveforms (volts) against A2_waveforms (volts) by a certain amount of time.
  • The waveforms are zero-centered and normalized such that the cross-correlation is bounded between [-1,1]. Zero means the waveforms are not aligned at all.
  • See cross_correlation_and_time_delay.pdf or, for details, scipy_correlate_behavior.pdf.

Definition at line 217 of file locate_signal.py.

_get_true_direction()

[float, float] _get_true_direction ( ROOT.pueo.Dataset dataset )

protected

Returns the true signal direction.

Parameters

[in]

dataset

The output of initialise.load_pueoEvent_Dataset

• Note that as stored in the .root files, the variable RFdir_payload is the direction the signal is travelling to.
• Therefore, to obtain the direction that the signal is coming from, we need the opposite vector.
• Thus, \(\phi_{\rm true} = (\phi_{\rm rfdir} + 180 ^\circ) \% 360^\circ\), and \(\theta_{\rm true} = 180^\circ - \theta_{\rm rfdir}\)

Definition at line 299 of file locate_signal.py.

plot_correlation_map()

None plot_correlation_map	(	pl.DataFrame	correlation_frame,
		str	plot_name,
			true_phi = None,
			true_theta = None )

Plots the reult of cross_correlate.

Parameters

[in]	correlation_frame	The output of cross_correlate
[in]	plot_name	Remember to specify file type
[in]	true_phi	(optional) from _get_true_direction
[in]	true_theta	(optional) from _get_true_direction

• Required columns in correlation_frame:
  1. correlation maps
  2. masks
  3. Pol
• Using only one antenna pair, one can find a band of peak correlation scores, see the plot in the file description.
• If we then sum over all antenna pairs, we would be able to identify a single peak:

Correlation Skymaps (summed over all antenna pairs)

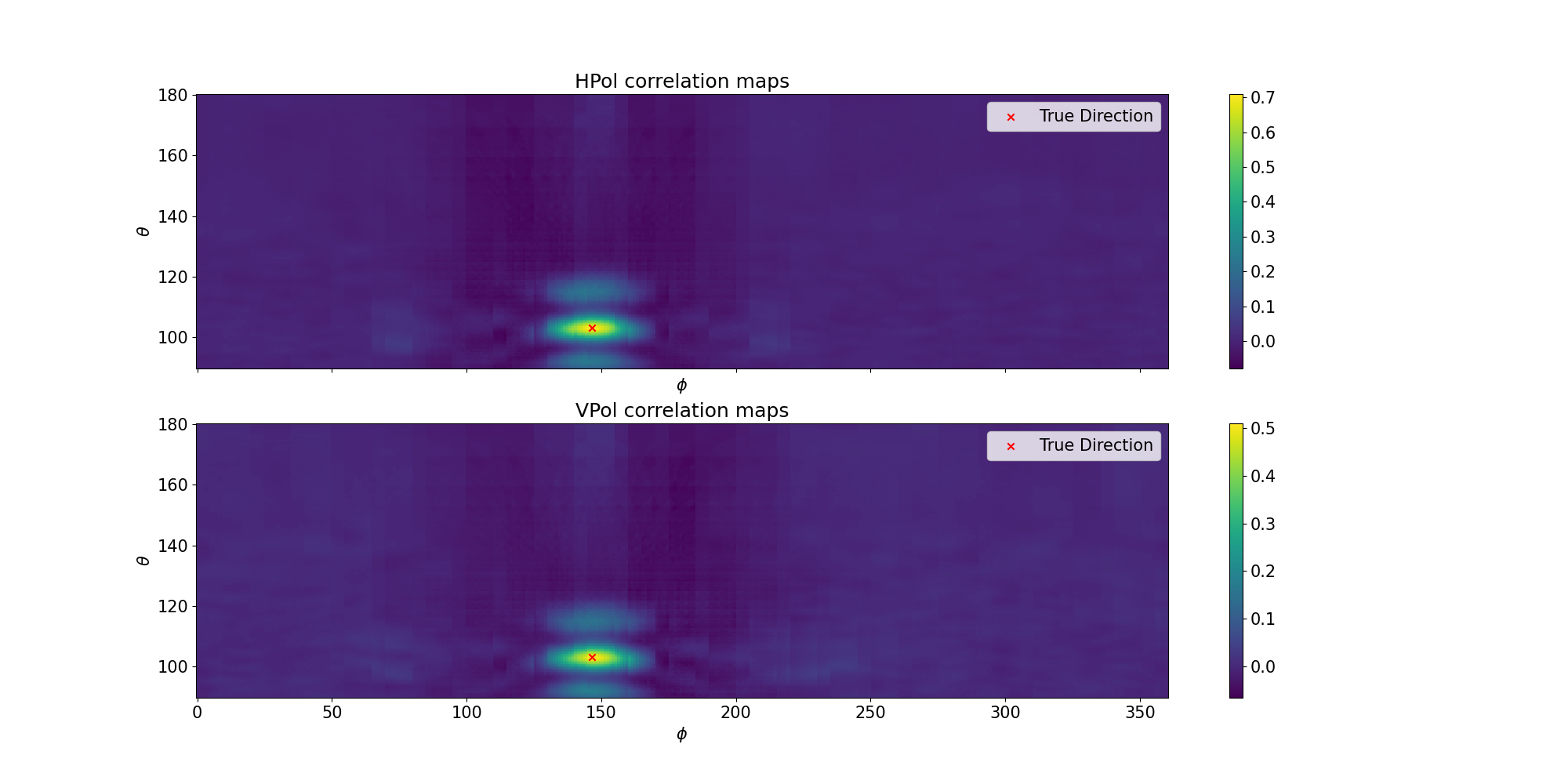
Definition at line 319 of file locate_signal.py.